nová adresa: http://ivo.pezlar.com/logika101/


Začínáme: Logika 101

„Je to logické.“ „Byl to jen další logický krok.“ „Má to svoji vlastní logiku.“ „Chováš se nelogicky.“... Tyto a jim podobné fráze slýcháme takřka denně. Co to ale vůbec je ta logika a k čemu je nám dobrá? To jsou otázky, které by měl být čtenář schopen sám zodpovědět po přečtení tohoto textu.

1. První krůčky

”Zločin je zcela běžný. Logika vzácná. Měl byste se proto zabývat daleko více logikou než zločinem. – Sherlock Holmes

Nejobecněji řečeno, logika je disciplína, která se zabývá usuzováním, resp. platnými úsudky. Úsudky se obecně skládají z výroků neboli tvrzení. Začneme odspodu a postupně si představíme, co je výrok, argument a nakonec, co je platný argument.

*Kromě výrazu „úsudek“ budeme také synonymně používat termíny „argument“, „odvození“ a „dedukce“.

1.1 Výroky

Zjednodušeně řečeno, výrok je každá věta (ať už napsaná nebo proslovená), u níž má smysl prohlásit, že je buď pravdivá, nebo nepravdivá. Příkladem výroku je tak např. tvrzení

Toto tvrzení může být pravdivé, nebo nepravdivé: pokud Alenka stojí vedle stromu, bude pravdivé, a pokud tam nestojí, bude nepravdivé. Žádná velká věda. Příklad dalších možných výroků:

Obecně tedy můžeme říci, že máme dvě velké skupiny výroků, a to pravdivé a nepravdivé. Do té první skupiny patří např. (a), (d). Mezi nepravdivé výroky spadá např.(b) a (c).

A samozřejmě ne každá věta je tvrzením. Například:

To jsou všechno nepochybně věty, ale už ne tvrzení. Rozkazovací věty jako (e) nejsou výrokem, neboť nemá smysl mluvit o pravdivosti či nepravdivosti rozkazů (rozkazovacích vět). Stejně tak je tomu i v případě tázacích vět jako (f) a vět přacích jako (g). Ani budoucí věty jako (h) nelze považovat za výroky, jelikož — jednoduše řečeno — neznáme budoucnost. Mohli byste namítnout: copak si nestačí počkat do příštího týdne, a teprve potom rozhodnout, zda je tato věta pravdivá, nebo ne? Bohužel ne, protože pak bychom ohodnocovali výrok „Tento pátek prší.“, nikoli původní „Příští pátek bude pršet.“

A nakonec ani v případě (i) nemá smysl mluvit o pravdivosti, protože nevíme, co se za proměnou x skrývá. Pokud dosadíme např. číslo 2, věta (i) už bude (pravdivý) výrok, ale pokud dosadíme např. číslo 7, už to bude výrok nepravdivý. Jinými slovy, věta (i) je pravdivá, nebo nepravdivá v závislosti na tom, co dosadíme za neznámou x. Takže dokud nevíme, co máme dosadit, nemá smysl mluvit o pravdivosti této věty, a tudíž není výrokem. Ale pozor, věta „Pro každé celé číslo x platí, že x menší než 5.“ je už výrokem, jelikož má smysl se bavit o jeho pravdivosti.

*Pozor, nenechte se zmást tím, že všechny výroky jsou oznamovací věty – opačně tento vztah totiž neplatí. Např. (i) je nepochybně oznamovací věta (koneckonců něco oznamujeme, a sice konkrétně to, že x je menší než 5), ale nikoli výrok, neboť nevíme, jaká hodnota má být za proměnnou x dosažena. Nelze tedy jednoduše říci, že výroky jsou oznamovací věty.

2. Logické spojky

Doposud jsme se seznámili jen s tzv. jednoduchými neboli atomickými výroky. Atomické výroky jsou takové výroky, které neobsahují logické spojky. Odpovědět přesně na otázku, co jsou logické spojky, není jednoduché a zde se spokojíme se zjednodušujícím vymezením logických spojek jako určitých nástrojů sloužících ke vzájemnému spojování dvou a více výroku, popř. k jejich popření.

Pokud tak učiníme, tj. spojíme-li dva či více atomických výroků dohromady pomocí logických spojek, popř. popřeme-li nějaký výrok, dostaneme tzv. složené neboli molekulární výroky. Co jsou to tedy ty tajemné logické spojky? Určitě je dobře znáte, koneckonců každý z nás je (resp. jejich analogie v přirozeném jazyce) denně nespočetněkrát užívá. Mezi logické spojky se tradičně řadí:

*Existují samozřejmě i další možné logické spojky, ale těmi se teď nemusíme znepokojovat a bohatě si vystačíme s těmito základními pěti.

*Někomu by se mohlo zdát podivné, že mezi spojky řadíme i negaci. Je to z toho důvodu, že, technicky vzato, negovaný výrok vznikne spojením původního výroku s „negátorem“, tj. se spojkou (či v tomto případě spíše přípojkou) „ne“, popř. „není pravda, že...“, která neguje daný výrok.

Logické spojky (někdy také nazývané jako výrokové spojky) tedy nejsou nic jiného než spojky mezi výroky. Ale pozor, přídavné jméno „logické“ tam není jen tak pro parádu. Zdaleka ne všechny spojky mezi výroky lze považovat logické. Uvažme např. spojku „protože“. Byť může být užita k propojení dvou a více výroků (např. „Alenka se bojí včel, protože ji v dětství pobodaly.“), vztah, který tím mezi výroky vzniká, není logický, ale spíše vysvětlující.

*Se spojkami jako „ale“, „nicméně“, „bohužel“ atp. můžeme zacházet jako s logickou spojkou „a“, neboť pokud se nad tím zamyslíme (a odhlédneme od pro nás teď nepodstatné „negativní“ příchutě, kterou tyto spojky s sebou nesou), řadí jen dva výroky vedle sebe.

Zatím to může znít vše velmi složitě, ale když si to představíme na konkrétních příkladech, bude hned jasné, že o nic komplikovaného se nejedná. Pojďme tedy na to. Vezměme si např. výroky (a) a (d) a ze seznamu logických spojek vybereme např. konjunkci (pro lepší názornost ji vyznačíme tučně, což platí i pro další příklady). Když to dáme celé dohromady, dostaneme:

Voilá! Máme svůj první molekulární výrok. Nebylo to tak těžké, že? Můžeme samozřejmě libovolně měnit jak logické spojky, tak i užité atomické výroky. Např.

Výrok (bc) se vám může zdát na první pohled nesmyslný. Vždyť tu přeci není žádná spojitost mezi výroky (b) a (c)? Máte samozřejmě pravdu, ale implikace nevyžaduje žádnou souvislost mezi výroky, dokonce ani jejich pravdivost. Implikaci si představte spíše jako tvrzení libovolných podmínek, a ty si můžete vymyslet, jaké chcete. Může to znít poněkud zvláštně, ale běžně se s tímto přístupem setkáváme. Uvažte např. výroky jako „Jestli je tohle nejlepší film století, tak já jsem čínský bůh srandy.“ nebo „Jestli Sparta dnes vyhraje, tam sním svou čepici.“ apod.

A samo sebou, takovéto molekulární výroky můžeme dále spojovat s dalšími výroky (ať atomickými či molekulárními) a vytvářet tak další (a ještě složitější) výroky. Např. pokud spojíme dva molekulární výroky (ad) a (bc) dohromady pomocí spojky ekvivalence, dostaneme:

Typ výroku se pak už ale nemění. Jinými slovy, ať je výrok složený ze dvou nebo sto výroků, pořád je to molekulární výrok.

*Je důležité si všímat toho, jakým způsobem byl molekulární výrok složený. Konkrétně v tomto případě výše se jedná o spojení výroků (ad) a (bc) spojkou ekvivalence. Na toto je třeba dávat pozor, neboť při letmém pohledu na složený výrok (adbc) by mohl někdo nabýt např. dojmu, že došlo ke spojení výroků (a) a (dbc) spojkou konjunkce.

3. Argumenty

Už jsme se seznámili s výroky (atomickými i molekulární), nyní jsou na řadě argumenty, které jsou z nich složené. Obecně řečeno, argument je jazykový prostředek, jehož úkolem je někoho o něčem přesvědčit (klidně i sebe sama, pak bychom mluvili spíše o úsudku). Argumenty se skládají ze dvou částí, a to předpokladů neboli premis a závěru. Premisy jsou obecně ta tvrzení, na kterých se s přesvědčovanou osobou shodneme, popř. které považujeme za pravdivé, závěr je pak to tvrzení, o kterém chceme tuto osobu přesvědčit. Jinými slovy, předpoklady jsou ty výroky, které mají podporovat či určitým způsobem zdůvodňovat závěr.

V běžném jazyce argumenty většinou rozpoznáme pomocí výrazů jako „z toho plyne“, „v důsledku toho“, „z toho vyplývá“, „takže“, „tudíž“, „tím pádem“, „tedy“ atp., které od sebe tyto dvě části, tj. premisy a závěr, oddělují. Např. „Tento vlak jede do Berlína. Berlín je hlavním městem Německa. Tudíž tento vlak jede do Německa.“

Uvažme ještě jeden příklad argumentu, tentokrát ve strukturovanější podobě, jaká je v logice zvykem:

V tomto argumentu vystupují výroky „Prší.“ a „Jestliže prší, pak je mokro.“ jako premisy a „Je mokro.“ jako závěr, který se tradičně odděluje horizontální čárou. Půvab (platných) argumentů jako ten výše spočívá v tom, že pokud náš oponent přijme premisy, pak musí uznat i závěr. Není totiž představitelné, že by mohly být pravdivé obě premisy a současně nebýt pravdivý závěr. Nastane-li taková situace, řekneme, že závěr vyplývá z premis, popř. že závěr je logickým důsledkem premis. A samozřejmě závěr jednoho argumentu nám může posloužit jako premisa pro další argument atd.

Samozřejmě ne v každém argumentu je závěr logickým důsledkem premis. Uvažme např. následující úsudek

Slovy „Alenka upustila sklenici, tudíž se sklenice rozbila.“ V tomto případě závěr nevyplývá z premis, jelikož si jistě dokážeme představit řadu situací, ve kterých je premisa „Alenka upustila sklenici.“ pravdivá, ale závěr „Sklenice se rozbila.“ nepravdivá. Alenka mohla například stát na takovém povrchu, který ztlumil pád sklenice (např. trampolína), popř. někomu se mohlo podařit zachytit sklenici ještě před tím, než dopadla na zem atp.

Můžeme tedy shrnout, že závěr „Sklenici se rozbila.“ nevyplývá z premisy „Alenka upustila sklenici.“ Ale pozor, tento závěr už vyplývá z premis „Alenka upustila sklenici.“ a „Jestliže Alenka upustila sklenici, sklenice se rozbila.“ Čím se tedy vyznačuje logický důsledek? Stručně řečeno tím, že je nepředstavitelné, aby nastala situace, kterou popisují premisy, ale nenastala situace, kterou popisuje závěr.

Na druhou stranu, určitě bychom se také zdráhali označit úsudek výše za nelogický. V určitém smyslu je „logické“ předpokládat, že každá upuštěná sklenici se rozbije, jelikož většina upuštěných sklenic se skutečně rozbije. Zde je ovšem výraz „logický“ užit v odlišném smyslu. Doposud jsme se zabývali výhradně jen tzv. deduktivním usuzováním, které se vyznačuje právě tím, že pravdivost premis zaručuje pravdivost závěru. Argument výše je ovšem příkladem spíše tzv. induktivního usuzování, kdy premisy slouží pouze jako „dobrý důvod“ pro přijetí závěru, ale přísně (deduktivně) vzato, z nich nevyplývá. Fiktivní detektiv Sherlock Holmes se proslavil právě tímto typem usuzování (ačkoli Holmes k němu odkazoval jako k dedukci, jednalo se o indukci).

Uvažme následující Holmesovu úvahu:

"Myslím, že mé úsudky jsou celkem potvrzeny. Pokud jde o přídavná jména, jichž jsem užil, řekl jsem, neklame-li mne paměť: přívětivý, prostý ctižádosti a roztržitý. Pokud sahá moje zkušenost, jen přívětivý člověk dostává na tomto světě dárky na památku, jen člověk prostý ctižádosti opustí londýnskou kariéru a jde na venkov a jen roztržitý člověk zanechá po hodině čekání ve vašem pokoji hůl místo navštívenky.“ (A. C. Doyle - Pes baskervilský, s. 391-392)

Ovšem jistě nejen přívětiví lidé dostávají dary s věnováním, na venkov se z města odchází ne vždy jen z nedostatku ctižádosti a jistě není problém představit si ani takového člověka, který někde zapomene svoji hůl, i když není roztržitý. To, co zde tedy známý detektiv z Baker Street praktikuje, není dedukce, ale indukce.

Tímto typem úsudků, kdy premisy nezaručují pravdivost závěru, ale spíše ho jen naznačují, se zde zabývat nebudeme. Jsou nepochybně neuvěřitelně užitečné (koneckonců, drtivá většina našich každodenních úsudků jsou právě tohoto typu), ale v logice chceme mít obecně jistotu, že závěr je nutně pravdivý, pokud jsou pravdivé premisy, a tu nám induktivní usuzování bohužel nemůže poskytnout.

3.1 Platný argument

Pokud závěr argumentu vyplývá z jeho premis, řekneme, že je to deduktivně platný argument nebo krátce jen platný argument. Jinými slovy, platný argument je takový argument, kde je závěr logickým důsledek premis. Anebo ještě jinak: platný argument je takový argument, ve kterém není možné, aby byly premisy pravdivé a závěr nepravdivý. To znamená, že pravdivost premis zaručuje pravdivost závěru. Pokud to tedy shrneme, argument

není (deduktivně) platný argument, kdežto

už je logicky platný argument. Rozdíl je tedy v tom, že zatímco v prvním případě můžeme přijmout pravdivost premis, ale odmítnout závěr (např. s námitkou „Co když ji upustila na trampolíně?“), v druhém případě již tuto možnost nemáme: pokud odsouhlasíme obě premisy, nezbývá nám nic jiného než souhlasit i se závěrem.

Neplatný argument je tedy takový argument, kde závěr nevyplývá nutně z premis. Všimněme si ovšem na první pohled poněkud podivné okolnosti. Uvažme následující úsudek:

Ačkoli se jedná o platný argument, může působit poněkud „nelogicky“. Proč by měla být schopnost slonů létat jakkoli závislá na tom, zda prší, nebo ne? To je přeci hloupost. To je samozřejmě pravda, ale vzpomeňme si na to, co jsme si řekli výše. Platný úsudek nedělají pravdivé premisy, ale ta okolnost, že za předpokladu, že jsou pravdivé premisy, musí být pravdivý i závěr. A tuto podmínku náš argument výše splňuje. Pokud je pravda, že prší a pokud je pravda, že jestliže prší, pak sloni létají, pak musí být pravda i to, že sloni létají. Pozor, opět zdůrazňuji, že platný argument neznamená pravdivý argument.

4. Krok směrem k formalismu

”Nic totiž není demokratičtější než logika. – Friedrich Nietzsche

Vzhledem k tomu, že při posuzování platnosti argumentů nás nezajímá konkrétní pravdivost výroků, nemusí nás zajímat ani jejich význam, neboť je to právě význam, podle kterého posuzujeme pravdivost toho či onoho výroku. A pokud odhlédneme či abstrahujeme od významu jednotlivých výroků, zbude nám jen jejich forma.

Domluvme se tedy, že atomické výroky, resp. jejich formu, budeme reprezentovat pomocí malých písmen \(p, q, \ldots \) atd., kterým budeme říkat výrokové proměnné. To znamená, že výroky (a) až (d) můžeme zapsat pomocí formálních znaků jako \(p, q, r, s\). Ale pozor, nezapomínejme, že se jedná o výrokové proměnně, tj. pokud to nebude nijak blíže určeno, písmeno \(p\) může zastupovat jakýkoli výrok, tzn. nejen všechny z (a)–(d), ale i libovolný další výrok. Výrokové proměnné tedy zastupují blíže neurčené výroky. Pro jednoduchost o nich budeme občas mluvit prostě jako o výrocích, tj. ne vždy budeme říkat „výroková proměnná \(p\)“, ale někdy pouze „výrok \(p\)“.

Dále se domluvme, že logické spojky budeme zkráceně zapisovat pomocí následujících symbolů:

* Často se můžeme setkat s odlišným značením těchto spojek, někdo např. používá místo \( \to \) symbol \( \Rightarrow \), popř. \( \supset \). Rovněž se také můžeme setkat např. s užívám symbolu \( \& \) místo \( \wedge \). V našem prostředí (tj. českém a slovenském) je ovšem zažité především značení uvedené výše.

Tím se dostáváme ke složeným neboli molekulárním výrokům. Složený výrok

tak můžeme formalizovat do podoby: kde \(p\) zastupuje výrok (a) a \(q\) výrok (d).

Zcela analogicky pak můžeme analyzovat

jako \( r \to s \) a úplně stejným způsobem bychom pokračovali i v dalších případech.

Nyní zkusme odhalit formu následujícího úsudku (vzpomeňme si při tom, co jsme si pověděli o logických spojkách a že argumenty se skládají z výroků):

Už by pro nás nemělo být těžké odkrýt, že forma tohoto argumentu je následující:

Řekli jsme si, že tento argument, resp. argument této formy, je platný, pokud nemůže nastat taková situace, kdy jsou předpoklady pravdivé a závěr nepravdivý. Co to ale znamená, když řekneme, že \( p \) je pravdivé, nebo že \( p \to q \) je pravdivé v našem nově zavedeném formálním prostřední?

4.1 Pravdivostní tabulka

Jak už víme, základní a v podstatě i jedinou charakteristikou výroků je to, že mohou být pravdivé, nebo nepravdivé. Zavedeme si tedy dvě tzv. pravdivostní hodnoty, a to Pravda a Nepravda, zkráceně P a N, resp. \( 1 \) a \( 0 \), které budeme používat zde (rovněž se můžeme setkat i se značením T a F odvozeným od anglických ekvivalentů True a False). Pokud bude nějaký výrok pravdivý, přiřadíme mu hodnotu \( 1 \), bude-li nepravdivý, přiřadíme mu hodnotu \( 0 \).

Uvedli jsme také, že konkrétní pravdivostní hodnota toho či onoho výroku nás vlastně přímo nezajímá. Co nás ovšem zajímá je to, že každý výrok \( p \) může nabývat buď pravdivostní hodnotu Pravda, nebo pravdivostní hodnotu Nepravda. Tuto situaci si můžeme ilustrovat pomocí tzv. pravdivostní tabulky:

\( p \)
\( 1 \)
\( 0 \)
Žádná jiná možnost nemůže nastat.

Co se ale stane, když uvážíme složené výroky? Začneme nejjednodušším způsobem, jak vytvořit složený výrok, tj. s pomocí negace neboli záporu. Pravděpodobně dokážete velmi dobře odhadnout, jak se bude taková spojka chovat, resp. jak bude vypadat pravdivostní tabulka pro výrok \( \neg p \) , tj. pro znegovaný výrok \( p \):

\( \neg \) \( p \)
\( 0 \) \( 1 \)
\( 1 \) \( 0 \)
Jednoduše řečeno, negace obrací pravdivostní hodnoty. To je koneckonců přesně takové chování, jaké bychom od negace očekávali. Je-li aplikována na pravdivý výrok, výsledek bude nepravdivý výrok a naopak. Kdy bude tedy výrok \( \neg p \) pravdivý, tj. nabývat pravdivostní hodnotu \( 1 \)? Právě tehdy, když \( p \) bude nepravda, tj. mít hodnotu \( 0 \) (viz tabulka výše).

Pojďme dále zkusit zkonstruovat pravdivostní tabulku pro konjunkci. Jak asi málokoho překvapí, konjunkce bude pravdivá jen v tom případě, kdy budou pravdivé oba její členy (konjunkty):

\( p \) \( q \) \( p \wedge q \)
\( 1 \) \( 1 \) \( 1 \)
\( 1 \) \( 0 \) \( 0 \)
\( 0 \) \( 1 \) \( 0 \)
\( 0 \) \( 0 \) \( 0 \)
To opět odpovídá našim intuicím ohledně toho, co spojka „a“ znamená a jak se užívá.

Nyní uvažme složený výrok (resp. výrokovou formuli) \( p \to q \), který tvoří druhou premisu v našem argumentu výše. Kdy bude tento výrok pravdivý? Pověděli jsme si, že tento výrok budeme číst jako „jestliže \( p \), pak \( q \).“ To znamená, že \( q \) budeme chápat v určitém smyslu jako následek \( p \). Uvažme nyní už dobře známý výrok „Jestli prší, pak je mokro.“, který má právě tuto formu. Kdy bude tento výrok pravdivý? Výroková formule obsahuje dohromady dvě výrokové proměnné, budeme tedy muset uvážit celkem čtyři možné případy, kterou mohou nastat.

Uvažme první případ, a to že (1) oba výroky jsou pravdivé, tj. prší, a pak bylo mokro. V tom případě nám nezbývá nic jiného než říci, že i výrok \( p \to q \) je pravdivý. Nyní uvažme, že sice (2) prší, ale není mokro. V tom případě musíme prohlásit, že výrok \( p \to q \) není pravdivý. Co když ale (3) neprší, ale přesto je mokro? Ohrozí to nějak pravdivost formule \( p \to q \)? Samozřejmě že ne. Skutečnost, že je mokro, ale nepršelo, v žádném případě nepopírá výrok, že jestliže prší, pak je mokro jednoduše z toho důvodu, že tento výrok netvrdí, že jediný způsob, jak může nastat mokro je déšť. Nějaký šprýmař mohl například pokropit celou ulici vodou. Krátce řečeno, to, že nastal důsledek bez avizované příčiny, nevyvrací skutečnost, že by mohl nastat i s avizovanou příčinou, tj. s \( p \). A na závěr uvažme poslední možnost, a to že ani (4) neprší, ani není mokro. Nastane-li takový případ, můžeme prohlásit, že \( p \to q \) je pravdivé z analogického důvodu jako v předchozím případě, jelikož o situaci, kdy neprší, se původní výrok vůbec nezmiňoval, a tak absence deště nemůže ovlivnit pravdivost výroku \( p \to q \).

Tabulka pro implikaci by tedy vypadala následovně:

\( p \) \( q \) \( p \to q \)
\( 1 \) \( 1 \) \( 1 \)
\( 1 \) \( 0 \) \( 0 \)
\( 0 \) \( 1 \) \( 1 \)
\( 0 \) \( 0 \) \( 1 \)

*Podobné tabulky lze samozřejmě zkonstruovat i pro ostatní logické spojky, které jsme si zde představili.

Toto zjištění je velmi užitečné, neboť příště, až narazíme na (pravdivé) výroky \( p \) a \( p \to q \), budeme vědět, že už můžeme rovnou tvrdit i nový výrok \( q \), jelikož z předchozích dvou nutně vyplývá. Tento poznatek můžeme dále zobecnit na všechny výroky: „Jestliže je pravda, že \( A \) a že \( A \to B \), pak můžeme tvrdit, že je pravda i \( B \).“, kde \( A \) a \( B \) nám zastupují libovolné výroky (tj. ať už atomické, nebo molekulární). To, co jsme nyní definovali, se obecně označuje jako odvozovací pravidlo, konkrétně odvozovací pravidlo vystupující pod jménem Modus ponens (krátce jako MP), popř. pravidlo odloučení, a schematicky se tradičně zapisuje jako

K čemu nám jsou odvozovací pravidla? Jednoduše řečeno, odvozovací pravidla nám dávají návod, jak odvodit z toho, co už víme, něco nového bez nutnosti zdlouhavě rozepisovat a zkoumat jejich pravdivostní tabulky.

Vzpomeňme si např. na náš první argument:

Je zřejmé, že odvození výroku „Je mokro.“ z výroků „Prší.“ a „Jestliže prší, pak je mokro.“ proběhlo v souladu s právě diskutovaným pravidlem MP. A vzhledem k tomu, že toto pravidlo zachovává pravdivost, jak jsme si už ukázali (tj. jsou-li pravdivé premisy, je pravdivý i závěr), jedná se o platný argument.

5. Užití a aplikace aneb od teorie k praxi

”Invence není výsledkem logického usuzování, ačkoliv finální produkt vykazuje logickou strukturu. – Albert Einstein

Seznámili jsme se se základními principy logiky (platný argument, logický důsledek, premisy, závěr, odvozovací pravidla...) a využitím formalismu, ale k čemu je nám to vše dobré? To se pokusíme demonstrovat na několika následujících příkladech.

5.1 Příklad I.

Uvažme následující argument:

Je tento úsudek platný? Všimněme si, že k tomu, abychom to rozhodli, nepotřebujeme vědět, co je brachiosaurus, sauropod nebo řád plazopánvích. Jinými slovy, i bez znalosti významu užitých termínů jsme schopni rozeznat, že tento argument byl odvozený prostřednictvím pravidla MP, a tudíž můžeme i tvrdit, že se jedná o platný argument.

Tento příklad pěkně demonstruje sílu a eleganci formálního přístupu. Můžeme totiž posoudit kvalitu daného úsudku, aniž bychom museli nutně znát význam všech použitých výrazů. To je obecně velká výhoda, neboť nemusíme být přímo odborníky v daném oboru, abychom byli schopni posoudit kvalitu argumentace. Můžeme si takto sami ověřit, zda závěr skutečně vyplývá z premis, anebo zda se jen někdo snaží např. vyvolat dojem promyšlené argumentace užíváním pro nás neznámých termínů.

5.2 Příklad II.

Uvažme následující logickou hádanku. Chceme zjistit, jestli Alenka spadla do králičí nory. Víme jen, že

Jak přistoupit k řešení takovéhoto problému? Ze všeho nejdříve si formalizujeme tyto čtyři předpoklady: nechť \( a \), \( b \), \( c \) po řadě označují výroky „Alenka spadla do králičí nory.“, „Barunka spadla do králičí nory.“ a „Cecilka spadla do králičí nory.“, pak dostaneme: Nás zajímá, jestliže \( a \), tj. jestli Alenka spadla do králičí nory. Jinými slovy, chceme zjistit, zda z těchto tří předpokladů vyplývá \( a \), tj. že není možné naleznout takovou situaci, ve které jsou všechny tři premisy pravdivé, tj. mají pravdivostní hodnotu \( 1 \), ale závěr, v našem případě \( a \), má hodnotu \( 0 \). Jak na to půjdeme? Asi nejjistější volbou bude zkonstruování pravdivostní tabulky. Ale co chceme přesně zjistit? Chceme se dozvědět, jestli existuje takové rozdělení pravdivostních hodnot, kdy \( a \) bude mít \( 0 \), a všechny tři premisy \( 1 \). A vzhledem k tomu, že nyní pracujeme se třemi výrokovými proměnnými, budeme potřebovat osm řádku, abychom pokryli všechny možné distribuce hodnot \( 1 \) a \( 0 \) mezi nimi.
\( a \) \( b \) \( c \) \( \neg a \) \( \neg b \) \( \neg c \) \( \neg a \to \neg b \) \( c \to b \) \( \neg c \to a \)
\( 1 \) \( 1 \) \( 1 \) \( 0 \) \( 0 \) \( 0 \) \( 1 \) \( 1 \) \( 1 \)
\( 1 \) \( 1 \) \( 0 \) \( 0 \) \( 0 \) \( 1 \) \( 1 \) \( 1 \) \( 1 \)
\( 1 \) \( 0 \) \( 1 \) \( 0 \) \( 1 \) \( 0 \) \( 1 \) \( 0 \) \( 1 \)
\( 1 \) \( 0 \) \( 0 \) \( 0 \) \( 1 \) \( 1 \) \( 1 \) \( 1 \) \( 1 \)
\( 0 \) \( 1 \) \( 1 \) \( 1 \) \( 0 \) \( 0 \) \( 0 \) \( 1 \) \( 1 \)
\( 0 \) \( 1 \) \( 0 \) \( 1 \) \( 0 \) \( 1 \) \( 0 \) \( 1 \) \( 0 \)
\( 0 \) \( 0 \) \( 1 \) \( 1 \) \( 1 \) \( 0 \) \( 1 \) \( 0 \) \( 1 \)
\( 0 \) \( 0 \) \( 0 \) \( 1 \) \( 1 \) \( 1 \) \( 1 \) \( 1 \) \( 0 \)

Jak se můžeme přesvědčit, v tabulce se nenachází takový řádek, ve kterém by \( a \) mělo hodnotu \( 0 \) a všechny premisy \( \neg a \to \neg b \), \( c \to b \) a \( \neg c \to a \) hodnotu \( 1 \). To znamená, že pokud tyto tři premisy budou pravdivé (a takový byl náš vstupní předpoklad), pak musí být pravdivé i \( a \), tj. Alenka doopravdy spadla do králičí nory. A skutečně, takových řádků se nám povedlo nalézt hned několik, konkrétně tři.

5.3 Příklad III.

Uvažme následující úvahu řeckého filozofa Platóna (cca 428 až 348 př. n. l.):

"Nejprve jest podle mého mínění stanoviti tuto rozluku: co jest to, co stále jest, ale vzniku nemá, a co jest to, co stále vzniká, ale nikdy není jsoucí? Ono lze chápati přemýšlením s pomocí rozumu, poněvadž je stále ve stejném stavu, toto může býti jen předmětem mínění s pomocí počitku bez účasti rozumu jakožto něco, co vzniká a zaniká, ale nikdy nemá pravé jsoucnosti. Dále všechno, co vzniká, vzniká nutně z nějaké příčiny, neboť jest nemožno, aby něco vzalo počátek bez příčiny. (…) Všechen pak svět (…), o něm jest nejprve uvážiti to, co musí býti předmětem počáteční úvahy při každé věci, zdali byl vždy a nemá žádného počátku svého vzniku, či vznikl a počal se z nějakého počátku. Vznikl, neboť je viditelný, hmatatelný a tělesný: všechna taková jsoucna lze číti, a co lze číti a chápati míněním s pomocí počitku, jest, jak se ukázalo, vznikající a časné. Ale co vzniklo, řekli jsme si, že nutně vzniklo z nějaké příčiny. (Platón - Timaios, s. 24)

Ačkoli se tato rozvaha může na první pohled zdát složitá až matoucí, v jejím pozadí je celkem jednoduchá argumentační (logická) struktura, kterou si nyní zkusíme rekonstruovat. Začneme identifikováním a mírným parafrázováním klíčových výroků, poté je formalizujeme a sestavíme celý odpovídající argument.

V prvním kroku tedy extrahujeme jednotlivé premisy:

Co z nich můžeme odvodit? Formálně by pak celý tento argument mohl vypadat např. následovně:
*Text za lomítkem slouží k záznamu toho, z čeho jsme daný řádek odvodili. Takže např. záznam "... / 4., 5., MP" si můžeme přeložit jako "Tento řádek byl odvozený z řádků 4. a 5. pomocí pravidla Modus ponens".

Krásná a jednoduchá ukázka užití MP v praxi. Jak se můžeme přesvědčit, i na první pohled poněkud kryptická pasáž stará více než 2000 let má v pozadí jednoduchou přímočarou logickou strukturu. Všimněme si, že jsme zde zužitkovali i poznatek z prvního příkladu, tj. nemusí nás trápit, když nevíme přesně, co Platón mínil termínem „jsoucí“, neboť platnost jeho argumentace jsme schopni zkontrolovat i bez této znalosti.

5.4 Příklad IV.

Doposud jsme uvažovali o \( p \) pouze jako o výroku a o symbolech \( 1/0 \) pouze jako o pravdivostních hodnotách Pravda a Nepravda. Není tu ovšem žádný důvod, proč se omezovat jen na tuto interpretaci. Co by se např. stalo, kdybychom \( p \) přestali pojímat jako výrok, který může být pravdivý, nebo nepravdivý, a místo toho jej chápali jako nějakou elektronickou součástku, kterou např. prochází nebo neprochází proud? Dnes už víme, co by se stalo: položili bychom základy rozvoje moderních počítačů schopných provádět úkony, o nichž se dříve myslelo, že jsou výhradně jen doménou lidí.

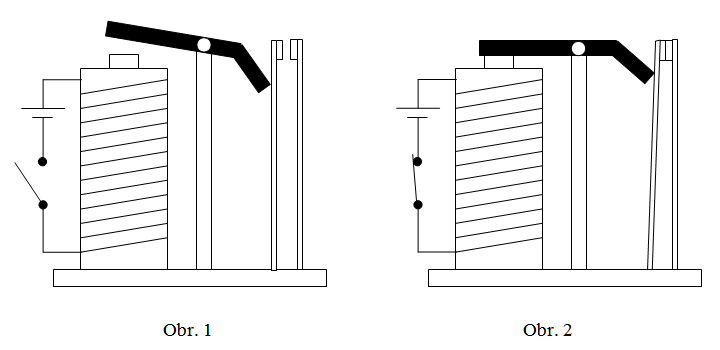
Ale ať to není jen teoretické povídání, pojďme se blížeji podívat na to, jak bychom mohli např. „naučit“ stroj používat logickou spojku „a“ neboli konjunkci. Ze všeho nejdříve se musíme seznámit s elektrotechnickou součástkou, které se říká elektromagnetické relé. To se skládá se z dvou obvodů, řídícího a řízeného. Říkejme jim Alfa a Beta. Řídící obvod Alfa spíná a přerušuje řízený obvod Beta. Obvod Alfa obsahuje cívku s jádrem z magneticky měkké oceli (tj. nezůstává trvale zmagnetizována). V její blízkosti je pohyblivá kotva rovněž z magneticky měkké oceli (viz obr. 1). Sepne-li se řídící obvod, cívkou začne procházet proud (řekněme o napětí 6 V), jádro se zmagnetizuje a přitáhne k sobě kotvu. Konec kotvy k sobě přitlačí pružné jazýčky spínače řízeného obvodu, a začne jím tak rovněž procházet proud (viz obr. 2).

Už víme, jak funguje relé, ale k čemu je nám to dobré? A co to má vůbec společného s logikou? To už uvidíme velmi brzy. Představme si nyní, že výrokové proměnné jako \( p, q, r \ldots \) nezastupují výroky, ale relé jako je to výše. To znamená, že \( p, q, r \) nebudeme číst jako výrok \( p \), výrok \( q \) atd., ale jako relé \( p \), relé \( q \) atd.

Dále jsme si také řekli, že relé se skládají ze dvou okruhů. Sepneme-li řídící obvod, zmagnetizuje se jádro a následně se sepne se i druhý, řízený obvod. To znamená, že relé v obvodu Alfa má vlastně dva možné stavy: zapnuto, nebo vypnuto. Přesněji, relé Alfa buď prochází proud, nebo neprochází. To ale přeci přesně koresponduje i s dalším aspektem výroků, tj. že mohou nabývat pouze dvě hodnoty: pravda, nebo nepravda. Analogicky, relé se může také nacházet ve dvou stavech: buď je sepnuté, nebo není.

Zjednodušíme si situaci a budeme uvažovat případ bez spínače, tj. obvod Alfa budeme spínat přímo přiložením 6voltové baterie a vypínat jejím odstraněním. V souladu s výše zmíněnou korespondencí si tedy předefinujme pravdivostní hodnoty \( 1 \) a \( 0 \), aby místo Pravda a Nepravda označovaly po řadě \( 6 \, \textrm{V} \) (= „zapnuto“) a \( 0 \, \textrm{V} \) (= „vypnuto“). Když tedy nyní řekneme, že \( p \) přidělíme hodnotu \( 1 \), máme tím vlastně na mysli, že relé \( p \) prochází elektrický proud o napětí \( 6 \, \textrm{V} \), a tím aktivujeme elektromagnet a v důsledku toho i řízený obvod.

Nyní si představme, že takováto dvě relé zapojíme sériově za sebe. Schematicky bude tato situace vypadat následovně:

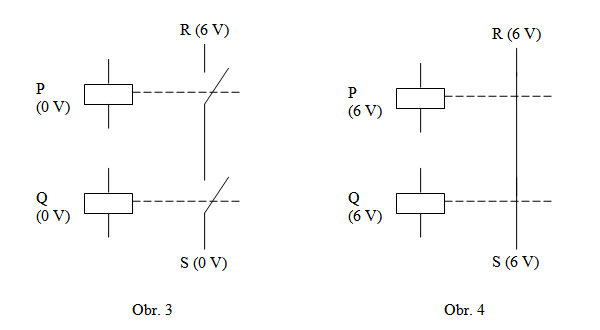
Dvěma sériově zapojeným relé říkejme \( P \) a \( Q \), obě jsou zatím neaktivní. Dále předpokládejme, že vstupní \( R \) část řízeného obvodu je pod napětím 6 voltů, výstupní část \( S \) je zatím bez proudu (viz obr. 3). Co se stane, když přiložíme 6voltové baterie k řídícím obvodům s relé \( P \) a \( Q \)? Oba jazýčky se sepnou, a to znamená, že proud bude nerušeně protékat až k \( S \), které bude nyní už také pod napětím 6 voltů (viz obr. 4). Ve všech dalších případech, tj. baterii přiložíme jen k jednomu z relé nebo k žádnému, bude napětí u \( S \) vždy 0 voltů. Pokud bychom si to chtěli shrnout v přehledné tabulce:

\( P \) \( Q \) \( S \)
\( 6 \, \textrm{V} \) \( 6 \, \textrm{V} \) \( 6 \, \textrm{V} \)
\( 6 \, \textrm{V} \) \( 0 \, \textrm{V} \) \( 0 \, \textrm{V} \)
\( 0 \, \textrm{V} \) \( 6 \, \textrm{V} \) \( 0 \, \textrm{V} \)
\( 0 \, \textrm{V} \) \( 0 \, \textrm{V} \) \( 0 \, \textrm{V} \)

Všimněme si, že tato tabulka přesně odpovídá tabulce konjunkce známé z dřívějška. Jinými slovy, obvod s dvěma seriově zapojenými relé vykazuje stejné chování jako bychom očekávali i u logické operace konjunkce.

Tímto jednoduchým způsobem lze tedy implementovat logickou spojku konjuknce. Obdobným způsobem pak můžeme sestrojit i negaci a disjunkci a za pomoci složitějších relé pak i další logické spojky.

*Jen pro zajímavost, byla to právě elektromagnetická relé, jež byla využita při konstrukci „usuzovacích“ mechanismů prvních elektromechanických počítačů, tj. ještě předtím než elektronky a tranzistory vstoupily na scénu. V mnoha dalších oblastech se využívají dodnes (např. v zabezpečovacích zařízeních na železnicích a tratích metra či v automobilech).

6. Závěr

”Logika, logika, logika. Logika stojí na začátku moudrosti, ne na jejím konci. – Spock

Tento text byl koncipován jako pouhá ochutnávka několika málo aspektů logiky, konkrétně tzv. klasické výrokové logiky. Rovněž třeba dodat, že velká řada témat, problémů a přístupů byla vynechána, a to málo, co zde bylo zmíněno, bylo velmi zjednodušeno. Naše příklady byly proto záměrně velmi různorodé, abychom demonstrovali co možná nejlépe široké pole působnosti logiky a ukázali, že jí nelze nikde uniknout. Kromě zmíněných oblastí má formální logika svoje místo např. i v matematice, informatice (umělé inteligenci, …), číslicové technice, lingvistice, právu, lékařství a dalších mnoha oborech, které si nárokují a vyžadují jasnost a přesnost. Logika je na nás zkrátka schopna vykouknout i z těch nejneočekávanějších míst, takže buďte vždy připraveni a ve střehu!

Citované zdroje:

Poděkování

Chtěl bych poděkovat Jiřímu Raclavskému za poznámky a korekce k dřívější verzi tohoto textu. (Poslední aktualizace obsahu: 9. 1. 2014; autor: Ivo Pezlar)